ลองถามใครๆ ดูก็ได้ว่า ‘เส้นทางที่สั้นที่สุดระหว่างจุดสองจุดมีลักษณะอย่างไร’
เรารู้ได้โดยสามัญสำนึกว่าคำตอบคือเส้นตรง แต่เหล่านักคณิตศาสตร์จะถามเรากลับว่ามั่นใจได้อย่างไรว่าคำตอบของเราถูกต้อง ในเมื่อเรายังไม่ได้ลองลากเส้นทุกเส้นที่เป็นไปได้
การไม่เห็นเส้นทางอื่น ไม่ได้หมายความว่าเส้นทางอื่นไม่มีจริง
******
เมื่อสามร้อยปีก่อน นักคณิตศาสตร์ชาวสวิสนามว่า โยฮันน์ แบร์นูลลี (Johann Bernoulli) ได้ตั้งกระทู้ถามในวารสารวิชาการว่า ‘หากต้องการสร้างรางเชื่อมระหว่างจุดสองจุด แล้วกลิ้งวัตถุเล็กๆ มาตามราง รางต้องมีลักษณะอย่างไรเพื่อให้วัตถุใช้เวลาน้อยที่สุดในการกลิ้งจากจุดหนึ่งมายังอีกจุดหนึ่ง’

ปัญหานี้มีชื่อว่า Brachistochrone Problem ซึ่งหากคิดด้วยสามัญสำนึกอย่างรวดเร็ว หลายคนอาจจะตอบว่ารางควรจะเป็นเส้นตรงเชื่อมระหว่างสองจุด เมื่อกลิ้งวัตถุลงมาแล้วจึงจะใช้เวลาน้อยที่สุด

แต่ในความเป็นจริง นักคณิตศาสตร์หลายคนในยุคนั้นคำนวณจนพบคำตอบว่ารางที่เป็นเส้นโค้งไซคลอยด์ (cycloids) ต่างหากที่จะทำให้วัตถุกลิ้งโดยใช้เวลาน้อยที่สุด
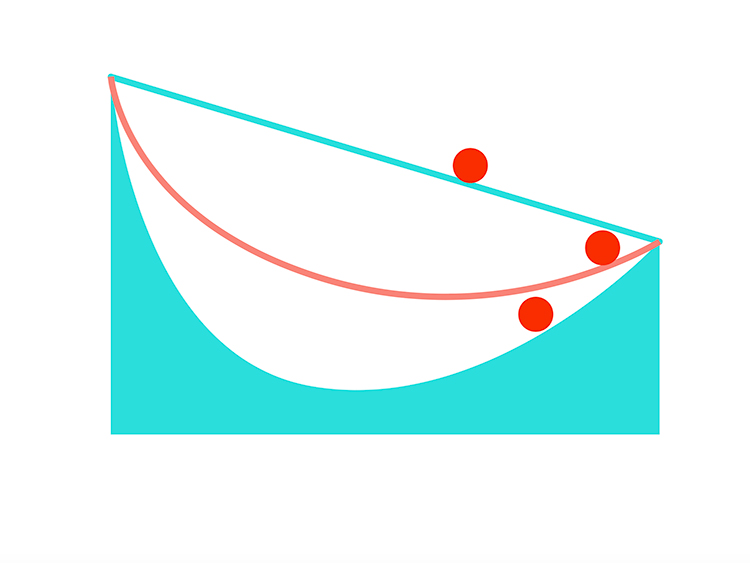
ในภาพนี้โค้งไซคลอยด์คือเส้นสีแดง ซึ่งวัตถุจะกลิ้งลงมาอย่างรวดเร็วเนื่องจากถูกแรงโน้มถ่วงดึงจนความเร็วเพิ่มขึ้นอย่างมากทำให้มาถึงปลายทางก่อนเส้นตรงที่วัตถุจะกลิ้งมาแบบสบายๆ แต่ถ้าใช้โค้งลักษณะอื่นที่โค้งมากกว่าไซคลอยด์จะพบว่าต้องใช้เวลามากขึ้นเพราะระยะทางที่เพิ่มมากจนส่งผลให้มันถึงจุดหมายช้าลงนั่นเอง
เรื่องน่าสนใจอย่างหนึ่งในประวัติศาสตร์คือ ในขณะที่นักคณิตศาสตร์คนอื่นๆ พยายามแก้ปัญหานี้ มีจดหมายฉบับหนึ่งส่งคำตอบมายังแบร์นูลลีอย่างรวดเร็ว ชายผู้นี้เห็นคำถามนี้ในช่วงเวลาเย็นและใช้เวลาทั้งคืนคิดหาคำตอบ (ในขณะที่นักคณิตศาสตร์คนอื่นในยุคนั้นใช้เวลาร่วมปี) ที่น่าทึ่งที่สุดคือวิธีการที่ชายผู้นี้ใช้แก้ปัญหาข้อนี้เป็นคณิตศาสตร์แขนงใหม่ที่ไม่เคยมีใครพบเห็นมาก่อน
ชายผู้นี้มีนามว่า เซอร์ ไอแซก นิวตัน ผู้คิดค้นคณิตศาสตร์สาขาที่เรียกว่า แคลคูลัสของการแปรผัน (calculus of variations) มาแก้ปัญหาข้อนี้ภายในเวลาหนึ่งคืน
วิชาแคลคูลัสของการแปรผันสามารถใช้พิสูจน์ได้ว่าเส้นที่สั้นที่สุดระหว่างจุดสองจุดคือเส้นตรง และยังพิสูจน์ได้ด้วยว่าถ้าจุดสองจุดนี้ไม่อยู่บนแผ่น แต่ไปอยู่บนผิวลักษณะอื่นๆ อย่างทรงกระบอก เส้นที่สั้นที่สุดระหว่างสองจุดจะเป็นโค้งรูปอะไร
ลองดูปัญหาคลาสสิกอีกข้อหนึ่ง
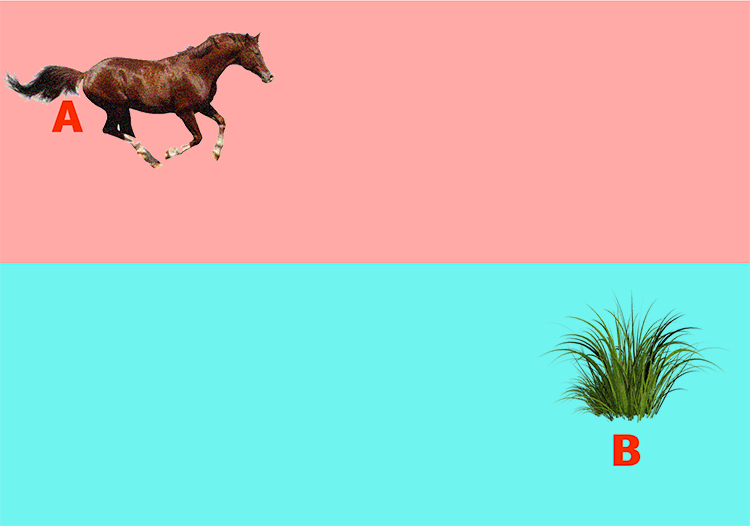
ถ้าม้าตัวหนึ่งยืนที่จุด A และต้องการวิ่งมากินอาหารที่จุด B เส้นทางการวิ่งของมันจะต้องเป็นอย่างไร หากในบริเวณสีน้ำตาลที่มันยืนอยู่ในตอนแรกนั้น เป็นพื้นดินที่มันสามารถวิ่งได้อย่างรวดเร็วด้วยความเร็วคงที่ค่าหนึ่ง แต่เมื่อวิ่งเข้าสู่บริเวณสีฟ้า มันจะวิ่งได้ช้าลงเนื่องจากเป็นพื้นที่ที่มีน้ำขัง
หากคิดเร็วๆ อาจจะตอบว่าม้าก็ควรจะวิ่งเป็นเส้นตรงจาก A มา B (เส้นสีชมพู) แต่หากใช้วิชาแคลคูลัสของการแปรผันมาคำนวณจะพบว่าคำตอบที่ได้เป็นเส้นสีแดง คือม้าจะต้องวิ่งในพื้นที่สีชมพูที่วิ่งได้เร็วให้มากกว่าไปวิ่งในพื้นที่สีฟ้าที่ตนวิ่งได้ช้า (แต่แน่นอนว่าต้องไม่วิ่งในพื้นที่สีชมพูมากเกินไปจนเสียเวลาไปกับระยะทาง)
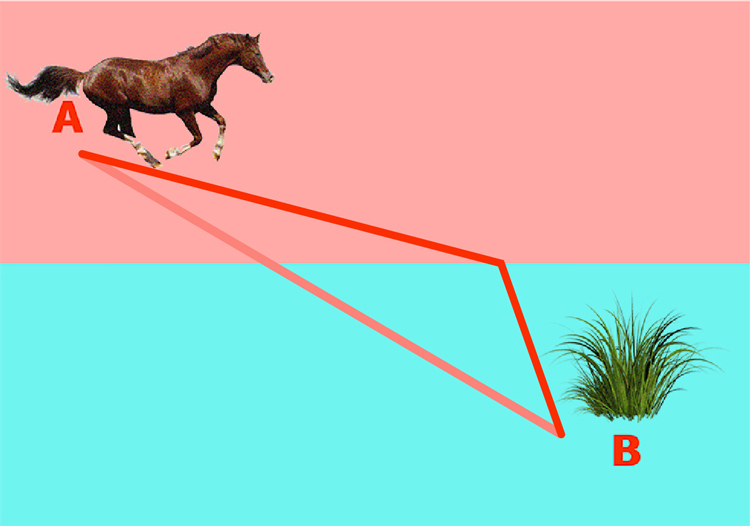
ความน่าสนใจคือ เส้นสีแดงที่ม้าวิ่งนั้น เป็นไปตามกฎฟิสิกส์เดียวกับการวิ่งของแสงจากอากาศแล้วผ่านลงไปในน้ำ แล้วเกิดการหักเหอย่างพอดี
ดาวิด ฮิลแบร์ท (David Hilbert) นักคณิตศาสตร์ผู้ปราดเปรื่องชาวเยอรมันผู้ค้นพบสมการหลักในทฤษฎีสัมพัทธภาพทั่วไปก่อนไอน์สไตน์ (แต่เขาให้เครดิตไอน์สไตน์เพราะไอน์สไตน์เป็นผู้เกาะติดเรื่องนี้มาโดยตลอด) กล่าวในช่วงปี 1900 ว่านักคณิตศาสตร์ควรพัฒนาแคลคูลัสของการแปรผันให้ก้าวหน้ายิ่งกว่านี้ เพราะก่อนหน้านั้นไม่มีงานวิจัยใหม่ๆ ในเรื่องนี้มากนัก
เรื่องทั้งหมดที่เล่ามานี้อาจเป็นเพียงแนวคิดสนุกๆ ของนักคณิตศาสตร์ที่ไม่ได้ส่งผลอะไรกับชีวิตประจำวันของเรา แต่หากมองให้ดีจะพบว่าสิ่งหนึ่งที่เราเห็นได้ในเรื่องนี้คือ ระยะทางที่สั้นที่สุดระหว่างจุดสองจุดนั้นเป็นเส้นตรงแน่ๆ
แต่เส้นตรงอาจไม่ใช่หนทางที่เร็วที่สุดเสมอไป
ภาพประกอบ ฟาน.ปีติ