400 ปีก่อนที่ประเทศเยอรมนี อัจฉริยะผู้มีนามว่า Johannes Kepler ใช้เวลาหลายปีขบคิดและวิเคราะห์ข้อมูลตำแหน่งดาวอังคารที่เพื่อนร่วมงานของเขาได้ศึกษาไว้ก่อนตาย จนค้นพบกฎการโคจรของดาวเคราะห์ที่ทุกวันนี้เราเรียกกันว่า ‘กฎของเคปเลอร์’ ซึ่งเด็กสายวิทย์ทุกคนต้องเคยเรียน
การวิเคราะห์ด้วยมันสมองเพียวๆ อย่างที่เคปเลอร์ทำนั้นเป็นงานที่หนักหนาสาหัสเอาการ
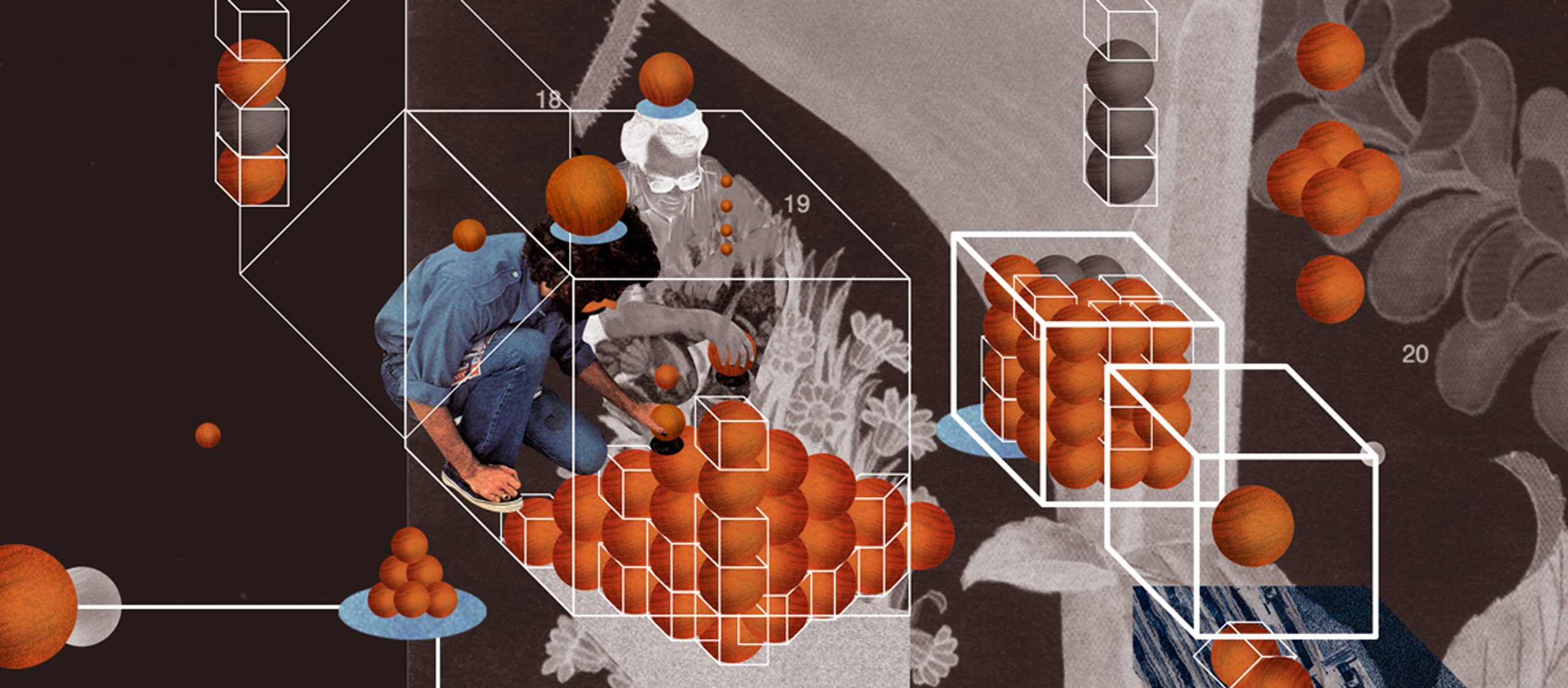
สิ่งหนึ่งที่หลายคนอาจไม่รู้คือ ช่วงหนึ่งของชีวิต เคปเลอร์เคยเผชิญกับปัญหาข้อหนึ่งที่ยากเย็นอย่างยิ่ง มันคือปัญหาที่ว่าจะจัดเรียงลูกกระสุนปืนใหญ่ทรงกลมในลังอย่างไร จึงจะสามารถบรรจุลูกปืนใหญ่ได้จำนวนมากที่สุด?
หากคิดโดยสามัญสำนึก คำตอบน่าจะเป็นการนำทรงกลมสามลูกมาเรียงชิดกัน แล้วนำลูกที่สี่มาไว้ซ้อนไว้ด้านบน จากนั้นเรียงในลักษณะนี้ไปเรื่อยๆเหมือนกับที่พ่อค้าแม่ค้าในตลาดเรียงผลไม้อย่างส้มเขียวหวานหรือแอปเปิลให้กองเป็นทรงพีระมิด การจัดเรียงในลักษณะนี้มีชื่อว่า ‘Hexagonal Close Packing’ ซึ่งเป็นการจัดเรียงที่มีประสิทธิภาพถึง 74.048 เปอร์เซ็นต์ (พูดอีกอย่างว่ามีที่ว่างเกิดจากการจัดเรียงนี้เกือบ 26 เปอร์เซ็นต์)
แต่เนื่องจากเคปเลอร์เป็นนักคณิตศาสตร์ เขาคิดว่าคำตอบที่ได้มาจากการคาดการณ์แบบนี้อาจไม่ถูกต้องก็ได้ เพราะการจัดเรียงทรงกลมนั้นมีวิธีการเรียงนับอนันต์
วิธีที่จะมั่นใจได้อย่างสมบูรณ์แบบว่าวิธีการเรียงแบบพ่อค้าขายส้มเป็นวิธีที่ดีที่สุดจริง ต้องทำการพิสูจน์ทางคณิตศาสตร์!
ปัญหาข้อนี้มีชื่อว่า ‘ข้อคาดการณ์ของเคปเลอร์ (Kepler Conjecture)’ เคปเลอร์เขียนถึงปัญหาข้อนี้ไว้ในหนังสือของเขาเมื่อ ค.ศ. 1611
ทว่าปัญหาที่ฟังดูเข้าใจได้ง่ายนี้กลับไม่สามารถแก้ได้โดยง่ายเลย เพราะหลังจากที่เคปเลอร์เสียชีวิต นักคณิตศาสตร์จำนวนมากพยายามแก้ปัญหานี้มาโดยตลอดแต่ไม่เคยมีใครแก้ได้ จนกระทั่งใน ค.ศ. 1900 David Hilbert นักคณิตศาสตร์อัจฉริยะจับปัญหาข้อนี้รวบรวมไว้ในชุดปัญหา 24 ข้อที่ท้าทายนักคณิตศาสตร์รุ่นใหม่ให้มาขบคิด
ต่อมาใน ค.ศ. 1998 นักคณิตศาสตร์ชาวอเมริกัน Thomas Callister Hales ประกาศว่าสามารถพิสูจน์ข้อคาดการณ์ของเคปเลอร์ได้ ด้วยบทพิสูจน์ที่ยาวกว่า 250 หน้า แต่การพิสูจน์ของเขาทำให้เกิดประเด็นดราม่าที่น่าสนใจขึ้น
เขาใช้วิธีพิสูจน์แบบที่ต้องพิสูจน์ไปทีละส่วน ซึ่งเป็นงานที่หนักหนามากๆ เขาจึงนำคอมพิวเตอร์มาช่วย แล้วส่งบทพิสูจน์นั้นไปยังวารสารวิชาการเพื่อรอรับการตีพิมพ์ คณะกรรมการจำนวน 12 คนได้ตรวจสอบความถูกต้องโดยใช้เวลานานกว่า 4 ปี จึงทำการประกาศผลว่า การพิสูจน์ของเขานั้นถูกต้องแน่ๆ 99 เปอร์เซ็นต์ ส่วนอีก 1 เปอร์เซ็นต์ เป็นเรื่องของโปรแกรมคอมพิวเตอร์ที่คณะกรรมการไม่สามารถตรวจสอบความถูกต้องได้
บทพิสูจน์ของเขาได้รับการตีพิมพ์ใน ค.ศ. 2005 ในวารสาร Annals of Mathematics ซึ่งมีชื่อเสียงมากในโลกคณิตศาสตร์
เมื่อเกิดปัญหาแบบนี้ขึ้น โทมัส เฮลส์ ซึ่งเป็นนักคณิตศาสตร์ย่อมไม่พอใจและไม่สบายใจที่การพิสูจน์ของเขาไม่ได้รับการยอมรับสมบูรณ์แบบ เขาได้รวมทีมงานจำนวนหนึ่งมาทำโครงการที่มีชื่อว่า Flyspeck Project ซึ่งจะคอยตรวจสอบการทำงานของโปรแกรมคอมพิวเตอร์ที่เขาใช้พิสูจน์ข้อคาดการณ์ของเคปเลอร์ทุกขั้นตอนอย่างละเอียด จนกระทั่ง ค.ศ. 2014 ทีมของเขาได้ประกาศว่าผลของความพยายามอันยาวนานได้สำเร็จ และเมื่อ ค.ศ. 2017 วารสารวิชาการด้านคณิตศาสตร์ Forum of Mathematics, Pi ได้มีการตีพิมพ์ผลงานการพิสูจน์ของเขาอีกครั้ง
ปัจจุบันนักคณิตศาสตร์จำนวนมากยอมรับว่าโทมัส เฮลส์ ได้พิสูจน์ข้อคาดการณ์ของเคปเลอร์แล้ว แต่บางส่วนก็อาจจะยังคลางแคลงใจ
อย่างไรก็ตาม นี่ไม่ใช่ครั้งแรกที่นักคณิตศาสตร์พยายามนำคอมพิวเตอร์มาช่วยในการคิดและพิสูจน์ทฤษฎีบททางคณิตศาสตร์ ก่อนหน้านี้ใน ค.ศ. 1976 มีการใช้คอมพิวเตอร์มาช่วยพิสูจน์ปัญหาทางคณิตศาสตร์เกี่ยวกับการระบายสีในแผนที่มาแล้ว และการนำคอมพิวเตอร์มาใช้ในการพิสูจน์ก็ไม่น่าจะเป็นครั้งสุดท้าย
คำถามจริงๆ ที่ซ่อนอยู่เบื้องหลังปัญหานี้คงเป็นคำถามที่ว่า ‘เราจะไว้ใจและเชื่อใจความคิดของคอมพิวเตอร์ได้แค่ไหน’ จนถึง ‘คอมพิวเตอร์สามารถเข้าใจแนวคิดเชิงนามธรรมทางคณิตศาสตร์ได้แค่ไหน’
นี่อาจเป็นปัญหาแท้จริงที่มนุษย์ต้องตอบให้ได้ก่อนที่คอมพิวเตอร์และปัญญาประดิษฐ์จะเข้ามาอยู่ในชีวิตประจำวันของพวกเรามากกว่านี้มากๆ ในอนาคตอันใกล้
อ้างอิง
https://arxiv.org/pdf/1501.02155.pdf
https://www.newscientist.com/article/dn26041-proof-confirmed-of-400-year-old-fruit-stacking-problem/
http://mathworld.wolfram.com/KeplerConjecture.html
http://mathworld.wolfram.com/Four-ColorTheorem.html